10212. Почти
кратчайший путь – взвешенный
Поиск
кратчайшего пути от начальной точки до конечной, с заданным набором точек и
длинами ребер их соединяющих, – уже хорошо известная задача. Это уже часть
нашей повседневной жизни, поскольку программы поиска кратчайшего пути широко
используются в наше время.
Большинству
людей эти приложения нравятся, поскольку они сильно облегчают их жизнь. А может
и не сильно.
Сейчас,
когда почти каждый имеет доступ к устройствам GPS-навигации, способным
рассчитывать кратчайшие пути, большинство маршрутов, образующих кратчайший
путь, становятся медленнее из-за интенсивного движения. Поскольку большинство
людей пытается следовать по одному и тому же пути, больше не стоит следовать
этим указаниям.
Имея
это в виду, Ваш начальник просит Вас разработать новое приложение, доступ к
которому будет иметь только он. Это сэкономит ему время на встрече или
каком-либо срочном мероприятии. Программа должна находить не кратчайший путь, а
почти кратчайший путь. Почти кратчайший путь – это такой кратчайший путь от
начальной точки до конечной, что ни одно его ребро не принадлежит какому-либо
кратчайшему пути между начальной и конечной точками.
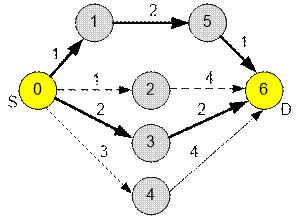
На
рисунке ниже представлена карта с кругами – точками местоположения, и стрелками
– односторонними маршрутами с указанными длинами. Начальная точка отмечена
как s, а конечная точка отмечена
как d. Жирные линии относятся к
кратчайшему пути (в данном случае имеются два кратчайших пути, каждый с
суммарной длиной 4). Почти кратчайший путь обозначен пунктирными линиями
(суммарная длина 5), поскольку ни один маршрут между двумя последовательными
точками не принадлежит ни одному кратчайшему пути. Обратите внимание, что может
существовать более одного возможного ответа, например, если маршрут
длиной 3 имеет длину 1. Ответ даже может не существовать.
Вход. Состоит
из нескольких тестов. Первая строка каждого теста содержит два целых числа n (2 ≤ n ≤ 500) и m (1
≤ m ≤ 104),
обозначающие соответственно количество точек на карте и количество существующих
односторонних маршрутов, соединяющих две точки. Каждая точка обозначается целым
числом от 0 до n – 1. Вторая строка
содержит два целых числа s и d, обозначающих соответственно начальную
и конечную точки (s ≠ d; 0 ≤ s, d < n).
Каждая
из следующих m строк содержит три
целых числа u, v и p (u ≠ v, 0 ≤ u, v < n, 1 ≤ p ≤ 103),
указывающих на существование одностороннего маршрута из u в v с расстоянием p. Существует не более одного маршрута
от точки u до точки v, но обратите внимание, что
существование маршрута от u до v не означает, что существует маршрут от
v до u, и, если такая дорога существует, она может иметь другую длину.
Последняя строка содержит два нуля и не обрабатывается.
Выход. Для
каждого теста выведите одну строку, содержащую -1, если невозможно
соответствовать требованиям, или целое число, представляющее длину найденного
почти кратчайшего пути.
|
Пример
входа |
Пример
выхода |
|
7 9 0 6 0 1 1 0 2 1 0 3 2 0 4 3 1 5 2 2 6 4 3 6 2 4 6 4 5 6 1 4 6 0 2 0 1 1 1 2 1 1 3 1 3 2 1 2 0 3 3 0 2 6 8 0 1 0 1 1 0 2 2 0 3 3 2 5 3 3 4 2 4 1 1 5 1 1 3 0 1 0 0 |
5 -1 6 |
РЕШЕНИЕ
графы –
алгоритм Дейкстры
Анализ алгоритма
Задан ориентированный
взвешенный граф, в котором выделены две вершины s и t. Пусть
величина кратчайшего пути от s к t равна d. Почти
кратчайшим путем от s к t называется такой путь наименьшей
стоимости, который не проходит ни по одному ребру, по которому может проходить
путь длины d. В задаче следует найти длину почти кратчайшего пути или
вывести -1 если такого пути не существует.
Запустим алгоритм
Дейкстры из вершины s на заданном графе и из вершины t на
обратном. Построим два массива dist и distR (dist Reverse), где
·
dist[i] равно длине кратчайшего пути от s
до i на исходном графе;
·
distR[j] равно длине кратчайшего пути
от t до j
на обратном графе;
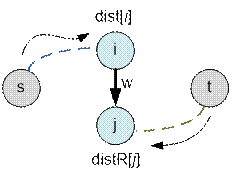
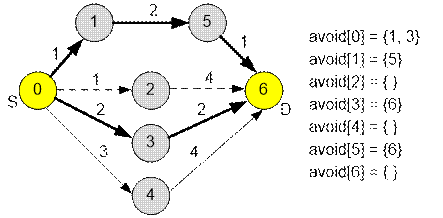
Все ребра, которые
могут лежать на кратчайшем пути, занесем в массив множеств avoid: avoid[i]
содержит такое множество вершин j, что через ребро (i, j)
длины w может проходить кратчайший путь. Это возможно, если только
имеет место равенство:
dist[i]
+ w + distR[j] == dist[t]
Осталось еще один раз
запустить алгоритм Дейкстры по ребрам, не входящих в avoid. Найденный путь и
будет почти кратчайшим. Его длина будет строго больше d.
Реализация алгоритма
Определим константы и рабочие массивы.
#define MAX 502
#define INF
0x3F3F3F3F
int parent[MAX];
vector<set<int>
> avoid;
Определим структуру ребра:
·
node – номер вершины в
которое идет ребро;
·
dist – длина ребра;
struct edge
{
int
node, dist;
edge(int node, int dist) :
node(node), dist(dist) {}
};
Функция сравнения ребер. Сортировка по возрастанию длин ребер.
bool operator< (edge a, edge b)
{
return a.dist
> b.dist;
}
Входной граф храним в списке смежности g. Обратный граф (ребра ориентированы в противоположную
сторону) храним в списке
смежности gr.
vector<vector<edge>
> g, gr;
vector<int>
dist, distR;
Ребра, соединяющие стартовую вершину с v,
заносим в вектор множеств avoid.
avoid[i] содержит такое множество вершин j, что через ребро (i,
j) может проходить кратчайший путь.
void path(int v)
{
if
(parent[v] == -1) return;
avoid[parent[v]].insert(v);
path(parent[v]);
}
Функция Dijkstra реализует алгоритм Дейкстры. Ей передаются список смежности графа g, массив кратчайших
расстояний dist, стартовая s и финальная f вершины.
int Dijkstra(vector<vector<edge>
> &g, vector<int>
&dist, int s, int f)
{
Инициализируем массив кратчайших расстояний dist.
dist = vector<int>(n,
INF);
dist[s] = 0;
Инициализируем массив предков parent (по нем будем восстанавливать путь от старта то заданно вершины).
memset(parent,
-1, sizeof(parent));
Объявим очередь с приоритетами pq. Заносим в нее стартовую вершину s, кратчайшее расстояние до которой равно 0.
priority_queue<edge>
pq;
pq.push(edge(s,
0));
while
(!pq.empty())
{
Из очереди с приоритетами pq извлекаем пару e. Значение e.node хранит номер текущей вершины, e.dist содержит расстояние
от стартовой вершины s до e.node.
edge e =
pq.top(); pq.pop();
int v =
e.node;
Если кратчайшее расстояние до финальной f уже посчитано, то заканчиваем
алгоритм.
if (v
== f) return dist[f];
Если вершина v = e.node является фиктивной (расстояние e.dist от начальной s больше уже
подсчитанного значения dist[v]), то пропускаем ее.
if
(e.dist > dist[v]) continue;
Перебираем вершины, смежные с v.
for (auto ed : g[v])
{
Рассматриваем ребро (v, to) длины cost.
int to =
ed.node;
int cost
= ed.dist;
Если ребро (v, to) лежит в avoid, то не рассматриваем
его.
if
(avoid[v].find(to) != avoid[v].end())
continue;
Если вершина to еще не включена во множество вершин,
кратчайшее расстояние до которых уже посчитано (used[to]
= 0), то
релаксируем ребро (v, to).
if (dist[v] +
cost < dist[to])
{
dist[to] = dist[v] +
cost;
pq.push(edge(to, dist[to]));
parent[to] = v;
}
}
}
Финальной вершины f мы так и не достигли, возвращаем -1.
return -1;
}
Основная часть программы.
Читаем
входные данные.
while (scanf("%d
%d", &n, &m), n + m)
{
scanf("%d
%d", &s, &f);
g.clear();
g.resize(n);
gr.clear();
gr.resize(n);
avoid.clear();
avoid.resize(n);
Читаем граф g. Строим обратный
граф gr.
for (i =
0; i < m; i++)
{
scanf("%d
%d %d", &b, &e, &w);
g[b].push_back(edge(e,
w));
gr[e].push_back(edge(b,
w));
}
Запускаем алгоритм Дейкстры из вершины s. Заполняем массив
кратчайших расстояний dist.
d =
Dijkstra(g, dist, s, f);
Запускаем алгоритм Дейкстры из вершины f по ребрам обратного графа. Заполняем массив кратчайших расстояний distR.
d =
Dijkstra(gr, distR, f, s);
Перебираем ребра графа (u, v). Те из них, которые
лежат хотя бы на одном кратчайшем пути, заносим в avoid.
for (u =
0; u < g.size(); u++)
{
for (i =
0; i < g[u].size(); i++)
{
v = g[u][i].node;
w = g[u][i].dist;
if
(dist[u] + w + distR[v] ==
dist[f]) avoid[u].insert(v);
}
}
Запускаем алгоритм Дейкстры из вершины s. Поскольку массив avoid уже не пуст, ищем
почти кратчайший путь – путь, который не проходит ни через одно ребро
кратчайшего пути.
d =
Dijkstra(g, dist, s, f);
Выводим длину почти кратчайшего пути.
printf("%d\n", d);
}